Funciones explícita e implícita
Hasta ahora, la mayoría de las funciones estudiadas se enunciaron de forma explícita. Por ejemplo, en la ecuación
la variable y está escrita explícitamente como función de x . Sin embargo, algunas funciones sólo se enuncian de manera implícita en una ecuación. Así, la función y = 1/x está definida implícitamente por la ecuación x.y = 1 . Supongamos que se pide calcular la derivada dy/dx para esta ecuación. Podemos escribir y como función explícita de x , y luego derivar.
|
|
|
|
|
|
|
|
Esta estrategia funciona siempre que se pueda despejar y como función de x en la ecuación, de lo contrario, este método no es viable. Por ejemplo, ¿cómo encontrar dy/dx para la ecuación
x2 - 2y3 + 4y = 2
donde resulta muy difícil despejar y como función explícita de x ? En tales situaciones se debe usar la llamada derivación implícita.
Para comprender esta técnica, es preciso tener en cuenta que la derivación se efectúa con respecto a x . Esto quiere decir que cuando se tenga que derivar términos que sólo contienen a x , la derivación será la habitual. Sin embargo, cuando haya que derivar un término donde aparezca y , será necesario aplicar la regla de la cadena , ya que se está suponiendo que y está definida implícitamente como función derivable de x .
Derivación implícita
Estrategias para la derivación implícita
-
1. Derivar ambos lados de la ecuación respecto de x .
-
2. Agrupar todos los términos en que aparezca dy/dx en el lado izquierdo de la ecuación y pasar todos los demás a la derecha.
-
3. Factorizar dy/dx del lado izquierdo de la ecuación.
-
4. Despejar dy/dx .
Observar que en el ejemplo 2 la derivación implícita puede producir una expresión para dy/dx en la que aparezcan a la vez x y y .
EJEMPLO N° 1
Encontrar dy/dx dado que y3 + y2 - 5y - x2 = - 4.
PASO N° 1: Derivar los dos miembros de la ecuación respecto de x.
PASO N° 2: Agrupar los términos con dy/dx en la parte izquierda y pasar todos los demás al lado derecho.
PASO N° 3: Factorizar dy/dx en la parte izquierda. (Factor Común)
PASO N° 4: Despejar dy/dx dividiendo entre (3y2 + 2y - 5).
Para ver cómo usar la derivación implícita, considerar la siguiente gráfica. En ella se puede observar que y no es una función de x . A pesar de ello, la derivada determinada en el ejemplo N° 1 proporciona una fórmula para la pendiente de la recta tangente en un punto cualquiera de esta gráfica.
EJEMPLO N° 1. AHallamos la pendiente de la recta tangente (En la gráfica, la línea AZUL) a la curva y3 + y2 - 5y - x2 = - 4 . en el punto P(2, 0):
|
|
La Pendiente de la recta tangente a la curva en cualquier punto P(x, y), viene dada por la ecuación:
|
|
Evaluemos la pendiente en el punto P(2, 0)
|
|
|
La pendiente de la recta tangente en el punto P(2, 0) es:
|
EJEMPLO N° 2
Encontrar dy/dx dado que xy + y2 + x2 = 1.
PASO N° 1: Derivar los dos miembros de la ecuación respecto de x.
PASO N° 2: Agrupar los términos con dy/dx en la parte izquierda y pasar todos los demás al lado derecho.
PASO N° 3: Factorizar dy/dx en la parte izquierda. (Factor Común)
PASO N° 4: Despejar dy/dx dividiendo entre (x + 2y).
EJEMPLO N° 1
EJEMPLO N° 2
EJEMPLO N° 3
EJEMPLO N° 4


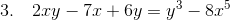



























LOOOOOOL
ResponderBorrar