DEFINICIÓN:
Una función racional está definida como el cociente de dos polinomios de la forma: f(x) = P(x) / Q(x) y simbólicamente lo expresamos de la siguiente manera:
EJEMPLOS:
CARACTERÍSTICAS:
Las gráficas de las funciones racionales pueden ser difíciles de dibujar. Para dibujar una gráfica de una función racional, puede tener en cuenta los siguientes aspectos: (SI NO HAY FACTORES COMUNES)
1. Interceptos con el EJE X: Son todos los puntos donde P(x) = 0
2. Interceptos con el EJE Y: Es el cociente entre a0 / b0
3. Asíntotas Verticales: Son todas las rectas donde Q(x) = 0
4. Asíntotas Horizontales: Verificamos el siguiente Teorema:
si m > n → Entonces no hay Asíntota Horizontal
si n = m → Entones en y = am / bn hay una Asíntota Horizontal
si m < n → Entonces en y = 0 hay una asíntota horizontal.
5. Asíntotas Oblicuas: Si NO hay Asintotas Horizontales y ademas se cumple que m - n = 1, Entonces existe una asíntota Oblicua LINEAL en P(x) / Q(x)
6. Cambio de signos: Los interceptos y las asíntotas definen los inte rvalos donde el signo cambia:
GRÁFICA DE LAS FUNCIONES RACIONALES:
Para iniciar la presentación, hacer click sobre ella, luego para ir avanzando la animación, click con la flecha derecha del teclado.
EJEMPLO N° 1
EJEMPLO N° 2
EJEMPLO N° 3
EJEMPLO N° 4
Ejemplo con Aisintptas Oblicuas.
SIMULADOR DE FUNCIONES RACIONALES
Esbozar la gráfica de las siguientes funciones Racionales:
| 1 |

|
= |
| 2 |

|
= |
| 3 |

|
= |
| 4 |

|
= |
| 5 |

|
= |
| 6 |

|
= |
| 7 |

|
= |
| 8 |

|
= |
| 9 |

|
= |
| 10 |

|
= |
11. y + 3xy = x2 + 1
12. 4xy + 2y = x2 + 5
| 13 | f(x) | = |
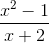
|
| 14 | f(x) | = |

|
| 15 | f(x) | = |
| 16 | f(x) | = |
| 17 | f(x) | = |
| 18 | f(x) | = |
| 19 | f(x) | = |
| 20 | f(x) | = |
| 21 | f(x) | = |
| 22 | f(x) | = |
| 23 | f(x) | = |















Cuál es la posible solución de la función 2/x^2 ?
ResponderBorrar