INTRODUCCIÓN::
Hasta ahora sólo hemos considerado límites de una función cuando x tiende a un número real a. Sin embargo, también podemos analizar el comportamiento de f(x), cuando x toma valores cada vez más y más grandes, sean estos positivos o negativos; es decir, cuando x → + ∞ (significa que “x” crece sin límite) o cuando x → - ∞ (significa “x” decrece sin límite). Esta clase de límites se denominan límites al infinito.
PROPIEDADES DE LOS LÍMITES :
Al evaluar límites al infinito, lo más seguro es que lleguemos a indeterminaciones matemáticas de la forma: ∞ / ∞, ∞ - ∞, 1∞, 0.∞, ∞0. Básicamente, trabajaremos las dos primeras.
Al evaluar el límite, debes tener en cuenta las propiedades de los límites que vimos en la tabla anterior y los siguientes dos TEOREMAS:
|
TEOREMA N° 1
|
TEOREMA N° 2, si n ∈ Z+
|
|
|
|
|
EN GENERAL
|
|
|
|
|
INDETERMINACIONES MATEMÁTICAS DEL TIPO
|
|

|
Si al evaluar el límite una función racional del tipo f(x) = g(x) / h(x) por sustitución directa obtenemos una indeterminación del tipo ∞ / ∞ , para eliminarla seguimos los siguientes pasos:
PASOS:
1. Comprobar la indeterminación – Aplicamos sustitución directa.
2. Dividimos cada término por la mayor potencia de x
3. Operamos algebraicamente y simplificando los término semejantes.
4. Aplicamos las propiedades de los límites.
5. Expresamos simbólicamente el límite.
TEOREMA: Límite de una función polinómica.
El límite de una función polinómica en el infinito es + ∞ ó - ∞, dependiendo de que el coeficiente del término de mayor grado del polinomio sea positivo o negativo:

|
Si an en POSITIVO.
|

|
Si an en NEGATIVO.
|
EJEMPLO:
|
Hallar el siguiente limite
|

|
Es una función polinómica, el limite es +∞, ya que el signo del coeficiente de la mayor potencia (2) es POSITIVO.
EJEMPLO:
|
Hallar el siguiente limite
|

|
Es una función polinómica, el limite es - ∞, ya que el signo del coeficiente de la mayor potencia (-4) es NEGATIVO.
EJEMPLO N° 1:
|
Hallar el límite de la siguiente función:
|

|
PASO N° 1: Aplicamos sustitución directa
Debemos eliminamos la indeterminación matemática
aplicando los pasos anteriores.
PASO N° 2: Dividimos cada término por la mayor potencia de x
PASO N° 3: Operamos algebraicamente y simplificando los término semejantes.
PASO N° 4: Aplicamos las propiedades de los límites.
PASO N° 5: Expresamos simbólicamente el límite.
CONTENIDO OCULTO
EJERCICIOS RESUELTOS
EJEMPLO N° 1
EJEMPLO N° 2
EJEMPLO N° 3
EJEMPLO N° 4
EJERCICIOS PROPUESTOS
| 1. |

|
| 2. |

|
| 3. |

|
| 4. |

|
| 5. |

|
| 6. |

|
| 7. |

|
| 8. |

|
| 9. |

|
| 10. |

|
| 11. |

|
| 12. |

|
| 13. |

|
| 14. |

|
| 15. |

|
| 16. |

|
| 17. |

|
| 18. |

|



























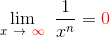














Esta muy bien explicado y los ejemplos son muy claros
ResponderBorrarMUY BUENA PÁGINA. FUE DE GRAN AYUDA. DIOS LES BENDIGA
ResponderBorrarMuy bien explicado, pero tengo una duda ¿El teorema número 2 nos permite resolver cualquier límite al infinito?
ResponderBorrartmb estas en el foro de la usmp?
BorrarEXCELENTE EXPLICACIÓN
ResponderBorrarpor fin pude encontrar una pagina que explica muy bien y esta organizado de la mejor forma , muchísimas gracias .
ResponderBorrarmuy buena pagina excelente,la unica pagina que dice lo que estoy buscando
ResponderBorrarChidoooo....!!!!
ResponderBorrar