INTRODUCCIÓN::
En algunas ocasiones al evaluar un límite reemplazando la variable por el valor al cual tiende se generan indeterminaciones del tipo .
Si al evaluar un límite nos encontramos con una indeterminación de esta forma, debemos proceder a eliminarla para poder establecer si el límite existe o no. Debemos trasladar el radical del numerador al denominador, o viceversa, factorizar, simplificar y volver a calcular el límite en la fracción simplificada.
| INDETERMINACIONES MATEMÁTICAS DEL TIPO |

|
Se pueden presentar DOS CASOS: |
2. Función IRRACIONAL.
CASO 2: FUNCIÓN IRRACIONAL :
Si al evaluar el límite una función irracional del tipo f(x) = √ g(x) por sustitución directa obtenemos una indeterminación del tipo 0 / 0, para eliminarla seguimos los siguientes pasos:
PASOS:1. Comprobar la indeterminación – Aplicamos sustitución directa.
2. Racionalizamos la expresión (Multiplicamos por el conjugado).
3. Operamos algebraicamente.
4. Simplificamos términos.
5. Evaluamos nuevamente el límite.
NOTA 1: Para raíces cuadradas, multiplicando el numerador y el denominador por el conjugado de la función irracional.
NOTA 2: Efectuar solamente la multiplicación de los binomios conjugados; lo demás, dejarlo indicado para facilitar la simplificación.
| EJEMPLO N° 1: : | Hallar el límite de la siguiente función: |
Debemos eliminamos la indeterminación matemática aplicando los pasos anteriores.
PASO N° 2: Racionalizamos la expresión (Multiplicamos por el conjugado).
PASO N° 3: Operamos algebraicamente.
PASO N° 4: Simplificamos términos.
PASO N° 5: Evaluamos nuevamente el límite.
PASO N° 6: Expresamos el límite.
| EJEMPLO N° 2: : | Hallar el límite de la siguiente función: |

|
Debemos eliminamos la indeterminación matemática aplicando los pasos anteriores.
PASO N° 2: Racionalizamos la expresión (Multiplicamos por el conjugado).
PASO N° 3: Operamos algebraicamente.
PASO N° 4: Simplificamos términos.
PASO N° 5: Evaluamos nuevamente el límite.
PASO N° 6: Expresamos el límite.
EJEMPLO N° 1 :
EJEMPLO N° 3 :
EJEMPLO N° 4 :


















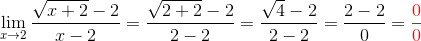




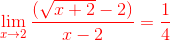





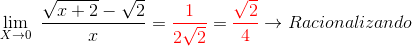

Muchas gracias , Dios te bendiga.
ResponderBorrar