INTRODUCCIÓN::
Hasta ahora sólo hemos considerado límites de una función cuando x tiende a un número real a. Sin embargo, también podemos analizar el comportamiento de f(x), cuando x toma valores cada vez más y más grandes, sean estos positivos o negativos; es decir, cuando x → + ∞ (significa que “x” crece sin límite) o cuando x → - ∞ (significa “x” decrece sin límite). Esta clase de límites se denominan límites al infinito.
PROPIEDADES DE LOS LIMITES:
Al evaluar el límite, debes tener en cuenta las propiedades de los límites que vimos en la tabla anterior y los siguientes dos TEOREMAS:
|
|
|
|
|
|
| INDETERMINACIONES MATEMÁTICAS DEL TIPO |

|
Si al evaluar el límite de una función irracional del tipo f(x) = √g(x) por sustitución directa obtenemos una indeterminación del tipo ∞ - ∞ , para eliminarla seguimos los siguientes pasos:
PASOS:1. Comprobar la indeterminación – Aplicamos sustitución directa.
2. Multiplicamos y dividimos por la conjugada.
3. Operamos algebraicamente y simplificando los término semejantes.
4. Evaluamos nuevamente el límite..
5. Expresamos simbólicamente el límite.
TEOREMA: Límite de una función polinómica.
El límite de una función polinómica en el infinito es + ∞ ó - ∞, dependiendo de que el coeficiente del término de mayor grado del polinomio sea positivo o negativo:

|
Si an en POSITIVO. |

|
Si an en NEGATIVO. |
EJEMPLO:
| Hallar el siguiente limite |

|
EJEMPLO:
| Hallar el siguiente limite |

|
| EJEMPLO N° 1: Hallar el límite de la siguiente función: |

|
PASO N° 2:Multiplicamos y dividimos por la conjugada:
PASO N° 3:Operamos algebraicamente y simplificando los término semejantes.
PASO N° 4:Evaluamos nuevamente el limite en la expresión resultante:
PASO N° 5:Expresamos simbólicamente el límite:
EJEMPLO N° 1
EJEMPLO N° 2


















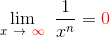





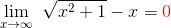
No hay comentarios.:
Publicar un comentario